DERESU-111

Domingo 4 de septiembre de 2011

He tratado de seguir el desarrollo del conflicto estudiantil chileno, gracias a diarios online. Como vivo en un país donde tres niveles de educación som responsabilidad de las comunas suecas, difícilmente yo podría decir que me opongo a la municipalización en general. Me refiero a la educación parvularia, primaria y secundaria.

La educación superior en Suecia es sin embargo responsabilidad del Estado.

Inicié este artículo el sábado 3 de septiembre de 2011, poco después de leer las primeras noticias sobre la tragedia aérea en Juan Fernández. Junto con sentir pena por los ausentes y solidaridad con las familias afectadas, no pude evitar recordar un grave accidente aéreo que me ocurrió al pilotear un avión del Club aéreo de la U. Santa María, en lejanos años de juventud.

Al continuar durante hoy domingo 4, he recordado también la única vez que he votado en una elección presidencial chilena. En ese inolvidable 4 de septiembre de 1970 acudí a las urnas junto a mi querido padre Rafael. El votó por don Jorge Alessandri y yo voté por don Salvador Allende.

La motivación principal de este escrito es que he leído en foros chilenos que la educación en diversos países es gratuita. Entre los ejemplos que se dan he visto paises como Argentina, Brasil y Finlandia. Con menor frecuencia he visto también a Suecia, como ejemplo de país que supuestamente ofrece gratuidad en la educación a sus habitantes.

Ignoro como son los sistemas educativos de los tres primeros países mencionados, pero considerando que a mí personalmente la educación sueca me sale ”un ojo de la cara”, no puedo estar de acuerdo con las personas que en diversos foros afirman que Suecia está entre los países con Gratuidad educativa.

Varias veces he mencionado en este blog que así como acostumbraba decír mi padre, ”Todo depende del cristal con que se mire”.

La afirmación sobre gratuidad me parece sin embargo tan incorrecta como si alguien afirmase que en Suecia el metal Oro es gratuito. Eso sin duda, nadie lo creería, ya que el metal oro se encuentra en un récord de precio internacional en US dólares. Por un lado hay preocupación bursátil y por otro la cotización del dólar se ha debilitado. Esa combinación fortalece la cotización del oro.

Siendo el oro un buen padrón internacional de precios, sumamente utilizado en tiempos de crisis cuando muchas organizaciones e individuos optan por vender partes de sus reservas monetarias para comprar oro, comencé este artículo con una imágen que representa 1 kg de oro sumamente puro. Tiene el previo sello del ahora fusionado Banco Unión de Suiza y ahí se puede comparar con el tamaño de una mano humana.

Como la densidad del oro es de 19,3 gramos por centímetro cúbico, entonces pesa 19,3 veces más que igual volúmen de agua. Es cosa de imaginar un envase de 1 litro de leche, pero lleno de agua, para conseguir estimar el tamaño de ese kilógramo de oro mostrado al principio. El litro de agua pesa 1 kg, mientras esa brillante barrita de oro pesa 1 kg. Su volúmen es entonces la 19,3 - ava parte del volúmen de un paquete de leche de 1 litro.

El litro de agua pesa 1 kg y equivale a un decímetro cúbico (o sea 10 x 10 x 10 = 1000 cm cúbicos). Un decímetro cúbico de oro pesa 19,3 kg.

============

El oculto Tesoro de Atahualpa

Una de las leyendas que más han estimulado la imaginación de muchos seres humanos en todo el mundo durante siglos, es la del escondido Oro de los Incas, en la forma del mitológico Oro del Rey Atahualpa. En Wikipedia encontré un artículo sobre el ”Tesoro de la Llanganatis”, donde se puede leer:

”Una versión de la leyenda sostiene que el general Inca Rumiñahui se dirigía a Cajamarca con un estimado de 750 toneladas de oro trabajado para el rescate, cuando supo que Atahualpa había sido asesinado. Sin embargo, la mayoría de los estudiosos creen que se trata de una sobrevaloración.

La única mención de una cantidad específica en los registros por soldado español Pedro Cieza de León, quien cita ‘300 cargas’. Una carga es la cantidad que un solo hombre podría llevar a grandes distancias y se estima en no más de 50 libras con lo que el tesoro contaría con menos de siete toneladas.”

Aquí se estima ese tesoro desde un mínimo cercano a 7 toneladas de oro, hasta un máximo de 750 toneladas de oro.

============

Adivinanza sobre Costo educacional

Ahora le propongo una adivinanza, basada en la suma de lo que cuesta en Suecia toda la educación parvularia, más toda la educación primaria, más toda la educación secundaria, durante unos 20 años.

Si un niño comienza en la escuela primaria a los 6 o 7, termina a los 18 o 19 después de 12 años de primaria y de secundaria aquí. Tal vez si repite un año llega a los 20. Como las guarderías también cuestan dinero, yo me baso en la suma del costo educacional durante 20 años, para todos los niños que van a las guarderías, escuelas y liceos en Suecia.

Cada año entra al sistema un número de bebés pequeños y cada año sale del sistema sueco un número de jóvenes con su título secundario. Eso permite imaginar una simplificación, consistente en que durante 20 años existe un número relativamente constante de alumnos.

Llamo a esa cantidad de ”Costo total de 20 años de educación pre-universitaria en Suecia”. Abrevio esa larga expresión y la llamo de ”CT-20-ES”.

Le propongo adivinar si ese  ”CT-20-ES” es totalmente gratuito, así como he leído que algunos foristas han afirmado en diarios chilenos online. Tal vez usted vé el asunto con otro prisma que yo.

Si en cambio usted no crée en la supuesta Gratuidad de esos 20 años de educación, le propongo entonces adivinar si el ”CT-20-ES” es inferior o superior al precio actual de 7 toneladas de oro. Ese es el nivel mínimo de oro en que se estima el famoso Tesoro de Atahualpa.

Si sospecha que el costo supera al equivalente a 7 toneladas del precioso metal, le propongo finalmente adivinar si el ”CT-20-ES” es inferior o superior al precio actual de 750 toneladas de oro. Ese el nivel máximo en que se estima el famoso escondido Oro de Atahualpa.

============

Oro chileno

En el sitio ”Infosur Hoy” encontré un artículo del 1 de Junio de 2011, donde se puede leer que Chile es el productor número 17 de oro en el mundo, con una producción cercana a las 40 toneladas de oro por año:

”By Claudio Espinosa for Infosurhoy.com—01/06/2011

Chile is ranked 17th in the global ranking of gold production, according to Bloomberg, with 39.494 metric tons in 2010, according to the Chilean Mining Ministry.”

Recordemos que en inglés esas 39.494 toneladas métricas equivalen a 39,49 toneladas en castellano, al cambiar punto decimal por coma decimal.

Para llegar a 750 toneladas de oro, que es el nivel máximo atribuído al oculto tesoro, se necesitaría un total de producción equivalente a casi 19 veces la producción áurea de Chile en el año 2010. 

============

Precio del oro

Buqué en Google por estos tres argumentos:
CNN Commodities Gold

El resultado alargado lo dividí en dos. Puse la mitad izquierda en la parte superior de la siguiente imágen:

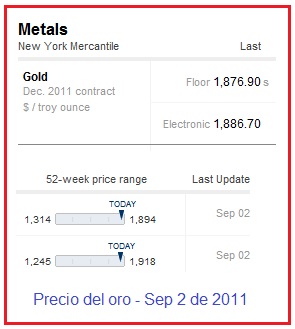
Se trata del nivel válido en New York el dia viernes 2, último dia hábil de la semana.

En la mitad inferior puse la parte derecha del resultado, donde se puede leer el rango de precios de las últimas 52 semanas.

Se puede leer que el precio máximo electrónico llegó a 1918 US dólares por onza (ounce) troy, el mismo viernes 2. En este caso la coma en 1,918 equivale a nuestro punto para 1.918

Este es el récord histórico en dólares, pero dí un vistazo a un diagrama sobre ”Inflation Adjusted Gold Price History” y noto que el precio real del oro parece haber tenido otro tope mayor alrededor de 1980.

Con esa reservación ya anotada, busco en Wikipedia por ”troy ounce” y me resulta la siguiente línea con otro punto decimal:

1 troy ounce = 31.1034768 grams

Divido el récord del viernes 2, de la siguiente forma:

1918 /  31,1034768 = 61,665132 US dólares por gramo de oro

Al multiplicar por 1000 obtenemos  61.665,132 US dólares por kilógramo de oro.

Llegamos a que el 2 de septiembre de 2011 el kg de oro costaba algo más de 61.600 US dólares.

============

Pesos chilenos

Busqué por el precio del US dólar y dí con la siguiente cotización:

”Valor del Dólar actual en Chile
Valor dia Sábado, 3 de Septiembre de 2011
1 Dolar = $ 460 Peso

============

1 kg de oro en pesos chilenos

Multiplicamos 61.665,132  x 460 y llegamos a 28.365.960 de pesos chilenos

1 kg de oro costaba unos 28 millones de pesos chilenos al 2 o 3 de septiembre de 2011.

============

Skatt, Impuesto y Tesoro

Como interesado en las sincronicidades puedo mencionar la palabra sueca SKATT, que puede significar Tesoro o Impuesto. En ese idioma son comunes las palabras compuestas. Sin profundizar en reglas gramaticales puedo agregar que la forma definida de Skatt es ”Skatten” (el impuesto o el tesoro).

”El tesoro de los Incas” se puede traducir a ”Inkaskatten”.

”El Impuesto Comunal” se conoce como ”Kommunalskatten”.

La coincidencia sobre la palabra SKATT me permite asociar el oculto tesoro de Atahualpa, con el Impuesto Comunal que cobran las 290 comunas suecas. Espero regresar a esa relación la próxima semana.

Mientras yo realizo algunas verificaciones, le propongo dar una mirada a la adivinanza descrita. Se trata en primer lugar de preguntarse si crée o no que la educación en Suecia es gratuita. En caso de no creerlo, se trataría de adivinar si el ”CT-20-ES” corresponde a menos o más que el precio actual de 7 toneladas de oro.

Y finalmente, en caso de suponer que en Suecia no existe la Gratuidad en la Educación y que su costo para una generación estudiantil de 20 años supera el valor de 7 toneladas de oro, se trataría de adivinar si ese costo es inferior o superior al precio de 750 toneladas de oro.

Para eso seguiríamos basándonos en los 28 millones de pesos chilenos por kg de oro a que llegamos poco antes en este artículo, o en algo más de 61.600 US dólares por kg de oro.

Temiendo haber cometido algún error (o varios) sobre uno o más múltiplos de 10, pido en ese caso disculpas anticipadas y termino con mi siguiente reservación de costumbre, es decir:

Salvo error u omisión.

Cordiales saludos
Rafael Meza