DERESU-111

Domingo 7 de marzo de 2010

Considerando que gran parte de los artículos archivados en este sitio sobre Deresu-111 se refieren a temas sobre Agua y Energía, quiero contribuir con un método práctico de calcular diferencias energéticas entre sismos. Los movimientos telúricos combinados con tsunamis están claramente relacionados con Agua y Energía.

Aprovecho de mencionar que la acumulación de ayuda solidaria destinada a los damnificados por el terremoto chileno del 27 de febrero de 2010, requiere de energía humana. Reunir dinero y ayuda material es comparable a las gotas de agua que se acumulan en cauces, que luego desembocan en los grandes rios.

Como chileno radicado en el exterior, hago lo que muchos compatriotas estamos haciendo en muchos países del globo. En mi país de residencia hay varias organizaciones actuando en favor de Chile y yo estoy apoyando a la Röda Korset (Cruz Roja). El mismo sabado 27 de febrero se destinaron los primeros 300.000 US dólares para apoyar el trabajo de 14 círculos locales de la Cruz Roja de Chile.

 

Este viernes 5 de marzo reciente se completaba el primer millón de US dólares reunido para Chile, por la Cruz Roja sueca. La meta es seguir acumulando recursos, hacer circular las alcancías e ir llenando las cuentas. El plan actual es por seis meses, que seguramente se prolongará por largo tiempo. Así como con las gotas de agua, con energía se irán sumando más y más aportes monetarios. Yo confío en que muchos millones de US dólares más irán llegando desde aquí hasta las zonas devastadas de Chile.

Desde muy lejos decimos también “Fuerza Chile”, contribuyendo con la solidaridad internacional demostrada en todas las naciones donde vivimos chilenos.

==========

Destrucción

Chile tiene el record mundial en Escala de Richter. Ningún país nos envidia ese récord.de Richter 9,5 ocurrido en ese inolvidable domingo 22 de mayo de 1960. Aquí incluyo la enorme marca roja que se vé en Google Earth:



 

Yo me encontraba a unos 450 km  a vuelo de pájaro, al nornoroeste de ese epicentro. Estaba en la función de matinée para niños, en el cine municipal de mi pueblo natal, cuyo empresario era mi padre. El inolvidable instante en que llegó el gran remezón, me dejó una impresión indeleble sobre los efectos de la energía que se transforma en las Megacatástrofes.

Hace una semana nuestro país sufrió los efectos de una nueva Megaconvulsión. Esta vez fué de 8,8 en la misma escala que midió el terremoto chileno de Richter 9,5 en 1960.

A lo largo de mi vida he tenido interés por problemas y soluciones relacionadas con Agua y Energía. Todo ello está a su vez asociado con mediciones y estimaciones. En el caso de los terremotos sabemos que se trata de escalas logarítmicas, pero basta mirar en Internet para encontrar innumerables contradicciones.

Me decidí por escribir este artículo, con la finalidad de llamar la atención sobre un exponente extra de 3/2 que explica muchos errores y que permite lograr cifras coherentes, con los logaritmos decimales y con la Escala de Richter.

========== 

Principio energético

La energía no se puede crear ni destruir, ya que solo se puede convertir.

Esa concisa formulación de la llamada “Conservación de la energía”, que se expresa además en la Primera Ley de la Termodinámica, implica que una forma de energía se puede transformar a otras formas de energía.

No se crea ni se destruye energía, pues solo se puede transformar energía. La energía de un terremoto se transforma en movimiento, roce, calor, luz, deformaciones, sonido, destrucción, etc. Esas vibraciones o desplazamientos afectan a todos los líquidos, inclusive el agua.

Un tsunami o maremoto es una de tantas formas en que se transforma la energía telúrica, que luego continúa transformándose hasta a miles de km de distancia del epicentro.

Es posible leer sobre la energía que se “disipa” con una explosión o con un temblor. Yo utilizaré a continuación los verbos disipar, transformar y convertir, al referirme a comparaciones energéticas entre diversas magnitudes Richter. 

==========

Cálculos y Calculadores

Unas pocas operaciones simples son de gran utilidad. Si usted ya dispone de un calculador apropiado, todo se simplifica aún más.

Si usted no tiene a mano un calculador apto, lo invito a mirar en mi artículo anterior que tiene el título “Usando un calculador cercano”. Ahí propongo usar el ejemplar que se encuentra en el propio sistema Windows de su PC.

He mostrado 5 ejemplos de operaciones, a los que he llamado “Tipo A” y respectivamente Tipo B, C, D y E.  Me valdré de esos ejemplos en las siguientes líneas.

==========

Diferencia de 1 grado de magnitud

Con los simples procedimientos explicados en “Usando un calculador cercano”, podemos ahora calcular la diferencia energética entre por ejemplo grado Richter 6 y grado Richter 5.

Primero comprobamos que la diferencia entre las magnitudes 6 y 5 es de 1 grado.

Enseguida elevamos el número 10 a su logaritmo 1, que es lo mismo que elevar 10 a su exponente 1. Aplicamos el ejemplo “Tipo A” y por supuesto nos resulta 10.

Finalmente elevamos ese resultado 10 al exponente 1,5, usando el mismo ejemplo “Tipo A“. Nos resulta lo siguiente:

31,622776601683793319988935444327

Esto significa que un sismo grado 6 disipa 31,62 veces más energía que un sismo grado 5.

Lo mismo ocurre al pasar de una magnitud Richter a la siguiente. Grado 7 es 31,62 veces más intenso que uno grado 6, mientras Grado 8 es 31,62 veces más poderoso que uno grado 7.

Todo esto es bien sabido, así es que no hay motivos para enojarse con algo tan elemental. Tal vez las ventajas de todo esto se vean un poco más adelante.

========== 
 

Diferencia de 2 grados de magnitud

Primero comprobamos que la diferencia entre las magnitudes 7 y 5 es de 2 grados.

Enseguida elevamos el número 10 a su exponente 2. Aplicamos el ejemplo “Tipo A” y por supuesto nos resulta 100.

Finalmente elevamos ese resultado 100 al exponente 1,5, usando el mismo ejemplo “Tipo A“. Nos resulta lo siguiente:

1000

Esto significa que un sismo grado 7 convierte 1000 veces más energía que un sismo grado 5.

==========

Conclusión para diferencias 1 y 2

La diferencia de intensidad (o de transformación energética) entre 2 grados de magnitud Richter, es de 1000 veces.

La diferencia de intensidad (o de conversión energética) con un grado de magnitud Richter, es de 31,62 veces.

Y eso se debe a que la raíz cuadrada de 1000 es justamente 31,62 seguido de todos los decimales que se indican anteriormente.

Al pasar de un grado Richter al siguiente aumenta la conversión en 31,62 veces. Eso hace que al aumentar en dos grados, se produce el cuadrado de 31,62 seguido de los demás decimales. Ese cuadrado conduce a 1000 veces. Y la raíz cuadrada de 1000 es 31,62.

==========

Diferencia entre Haiti 7,0 y Chile 8,8

Aunque no me es posible escribir notaciones aritméticas con este editor, puedo valerme aquí de una pequeña notación gráfica que hice aparte:

 

El terremoto chileno del 27 de febrero de 2010, transformó (disipó) 500 veces más energía que el sismo de Haití, el 12 de enero de 2010. He redondeado a 500, aunque se trata de poco más de 501. Aquí aplicaré el mismo procedimiento anterior.

Primero comprobamos que la diferencia entre las magnitudes 8,8 (Chile) y 7,0 (Haiti) es de 1,8 grados Richter. Ese 1,8 se acerca a 2. Hemos visto que una diferencia de Richter 2 equivale a 1000 veces. Siendo la escala Richter logarítmica, la diferencia equivalente a Richter 1,8 debería ser menor que 1000.

Para continuar, elevamos ahora el número 10 a su exponente 1,8. Eso lo marqué con amarillo en la formulita anterior. Aplicamos el ejemplo “Tipo A” y nos resulta:

63,095734448019324943436013662234

Finalmente elevamos ese resultado 63,09 y los demás decimales al exponente 1,5 usando el mismo ejemplo “Tipo A“. Nos resulta lo siguiente:

501,18723362727228500155418688495

El exponente final se expresa como 3/2 en la fórmula, pero para finalidades del cálculo simplifica elevar a 1,5.

Como las mediciones Richter son aproximadas, podemos redondear a 500.

Una diferencia de Richter 2 implica 1000 veces. Una diferencia de Richter 1,8 implica 501 veces.

==========

Exponente 3/2 o exponente 1,5

Este es el exponente extra que a veces se omite y que causa errores al aplicar la escala logarítmica directamente.

Hemos visto que la diferencia entre Richter 8,8 y Richter 7,0 es de 1,8. Si solamente aplicamos el antilogaritmo de 1,8 según el “Tipo C”, nos resulta 63,10.

Eso induce a pensar erróneamente que el terremoto de la Región Maule fué 63 veces más potente que el de Haití. Pero como nos falta elevar ello a 1,5 debemos continuar con una operación “Tipo A” más, hasta llegar a 501 veces.

Ese exponente extra 1,5 es muy importante y basta agregarlo a los cálculos logarítmicos, para que los resultados se ordenen con total coherencia.

==========

Diferencia entre Valdivia 9,5 y Haiti 7,0

Ahora que el mecanismo fué recientemente usado, podemos ir directamente al cálculo, de acuerdo a la siguiente fórmula:

 

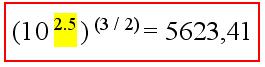
El terremoto chileno del 22 de mayo de 1960 disipó 5600 veces más energía que el terremoto de Haití (Enero de 2010). He redondeado a 5600, aunque se trata de poco más de 5623. Aquí aplico el mismo procedimiento anterior.

Primero comprobamos que la diferencia entre las magnitudes 9,5 (Chile en 1960) y 7,0 (Haiti en 2010) es de 2,5 grados Richter.

Sabemos que una diferencia de 2 implica 1000 veces. Por lo tanto una diferencia de Richter 2,5 debe conducir a más de 1000 veces.

Para saberlo con mayor precisión elevamos el número 10 a su exponente 2,5. Eso lo marqué con amarillo en la fórmula anterior. Aplicamos el ejemplo “Tipo A” y nos resulta:

316,22776601683793319988935444327

Finalmente elevamos ese resultado 316,22 y los demás decimales al exponente extra 1,5 usando el mismo ejemplo “Tipo A“. Nos resulta lo siguiente:

5623,4132519034908039495103977648

El exponente final se expresa como 3/2 en la fórmula, pero para finalidades del cálculo simplifica elevar a 1,5.

Como las mediciones Richter son aproximadas, podemos redondear a 5600 veces.

Una diferencia de Richter 2 implica 1000 veces. Una diferencia de Richter 2,5 implica 5623 veces.

==========

Reservaciones

Esos cálculos sobre energía disipada (convertida, transformada) no toman en cuenta ni la profundidad del epicentro, ni la distancia a determinada ciudad, ni el tipo de movimientos que adoptaron las ondas telúricas.

Estimaciones de otro tipo pueden aplicarse para calcular con unidades energéticos del tipo Joule, Kilocalorías o Megawatts-hora. Tal vez podría ser interesante comparar la energía transformada por un sismo, con la energía transformada por el agua cayendo por todas las turbinas de alguna central hidroeléctrica conocida. Esa tarea podemos dejarla para más adelante.

Lo que he mostrado es solo una indicación de lo que significaron ambos terremotos para nuestro querido Chile, tomando como referencia lo ocurrido en Haití en el mes de enero de 2010.

Dentro de un par de meses se cumplirán 50 años desde el mayor terremoto registrado en la Escala de Richter hasta el momento. Ese de grado 9,5 fué más de 11 veces más potente que el ocurrido recientemente en Chile con 8,8.

5623,41 / 501,19 = 11,22 veces

Muestro aquí una indicación del USGS (U.S. Geological Survey) que aparece en Google Earth. Copié la imágen y la reduje al 85% para que cumpliera con el maximo ancho permitido en este blog:

 

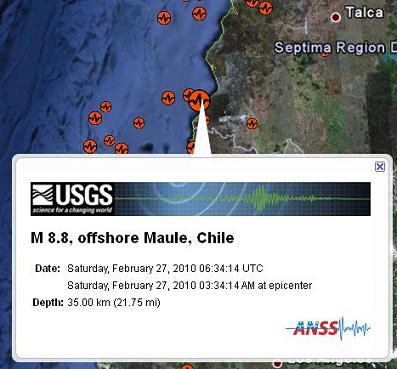
Resumiendo:

El reciente terremoto 8,8 de Chile en 2010 disipó 500 veces más energía que el de Haití 7,0.

El terremoto 9,5 de Chile en 1960 transformó 5600 veces más energía que el de Haití 7,0.

El terremoto 9,5 de Chile en 1960 convirtió más de 11 veces más energía que el de Chile 8,8 en 2010.

La fórmula aplicada más arriba se puede encontrar buscando por la Escala Richter. Agradezco de antemano cualquier corrección a mis cálculos.

Si por cualquier motivo usted considera que este tipo de comparaciones energéticas no se pueden hacer, yo le encuentro toda la razón. Como mi querido padre acostumbraba decir, “todo depende del cristal con que se mire”.

Salvo error u omisión.

Cordiales saludos
Rafael Meza

Domingo 7 de marzo de 2010

Muy pronto espero agegar un artículo sobre las diferencias energéticas entre sismos de variadas magnitudes Richter. Para ello se requieren unas pocas operaciones matemáticas que a su vez dependen de un calculador adecuado. Si usted se interesa por esas diferencias de potencia telúrica y tiene a su alcance un calculador de ese tipo, entonces podrá practicar los cálculos sin necesidad de leer este artículo.

Si usted no tiene un tal calculador a la mano, yo le propongo valerse del calculador que muy probablemente ya se encuentra en el computador que usted está usando. Si usa otro sistema operativo, asumo que le será fácil ubicar allí un aparato similar al que se encuentra en Windows.

Es cosa de escoger la versión avanzada, para que aparezca la siguiente configuración, con textos en el idioma correspondiente a cada instalación. En este ejemplo se trata de textos en sueco:

 

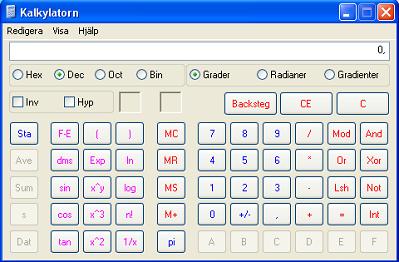
La imágen mostrada tiene sus lados reducidos en un 83% con respecto a lo que se vé en mi versión Windows casera, debido a que es el máximo ancho aceptado por este blog. Espero que a pesar de los símbolos comprimidos, usted consiga ver bien todas las letras, cifras y signos.

==========

Exponentes y Logaritmos

Ningún lector necesita irritarse si lo que escribo aquí ya es super conocido. Mi intención es solo mostrar un procedimiento simple para realizar algunas pocas operaciones. Quien tenga familiaridad con este calculador, puede saltarse mis explicaciones sin mayores problemas. Quien no tenga familiaridad con este aparatito, no pierde mucho con leer algunas líneas y ver unas pocas imágenes que simplificarán la lectura de mis demás aclaraciones, relacionadas con la Escala Richter.

Ahora copiaré la parte izquierda de la imágen anterior, con el tamaño normal que se vé en mi pantalla. Ahí utilizo tres circunferencias para destacar tres botones útiles más adelante:

 

El anillo azúl superior izquierdo encierra un cuadrado con el que es posible seleccionar la función “Inv”, para hacer el inverso de ciertas operaciones.

El anillo rojo del medio encierra la letra x seguida por un acento circunflejo ^ y acompañada por la letra y. Ese botón x^y se utiliza para seleccionar exponentes.

El anillo verde claro encierra las letras “log”. Ese botón es para seleccionar un logaritmo decimal.

Aquí agrego una imágen aumentada en 30% y que muestra la Inversión sin selección o con selección. También se muestran los botones para “x elevado a y” (exponente) y para logaritmo:

 

==========

Algunos ejemplos

Este editor no acepta notaciones matemáticas o fórmulas, así es que me valdré de textos.

Ejemplo Tipo A. Para calcular 2 elevado a 3, se comienza escribiendo 2 en la ventanilla superior tradicional. Enseguida se presiona el botón de exponente, es decir x^y. Luego se presiona el número 3. Finalmente se presiona el signo = (igual) que hace aparecer el resultado 8.

Pido disculpas por lo elemental de todo esto, pero una pequeña aclaración no daña a nadie, aunque sea sumamente redundante.

Tipo B. Para calcular el logaritmo decimal de 3 se escribe primero 3 en la ventanilla superior. Luego se presiona la tecla “log”. El resultado aparece directo, es decir 0,477. El calculador lo muestra con varios decimales::

0,47712125471966243729502790325512

Tipo C. Para calcular el antilogaritmo de 4 se comienza escribiendo 4 en la pantallita superior. Luego se marca al lado izquierdo de “Inv”. Enseguida se presiona “log”. El resultado es 10000.

La inversa de este antilogaritmo implica que el logaritmo decimal de 10000 es 4. Por lo tanto, si elevamos el número 10 a su exponente 4 mediante el ya descrito “Tipo A”, nos resulta 10000.

========== 

Raíces

Se utiliza la inversa del botón para exponentes.

Ejemplo Tipo D. Para calcular la raíz cúbica de 1000 se comienza escribiendo 1000 en la ventanilla superior. Enseguida se marca el cuadradito para “Inv”. Luego se presiona la tecla de exponente, es decir x^y. Enseguida se escribe 3 en la ventanilla. Finalmente se presiona el signo igual =. El resultado es por supuesto 10.

E
l Tipo D acepta exponentes con decimales. Por ejemplo, la raíz 1,5 de 1000 es 100.

Ejemplo Tipo E. Hay otra forma de calcular raíces tan comunes como las cuadradas o cúbicas, ya que hay botones para x^2 y para x^3. Haciendo el inverso de esas funciones, se logran las raíces. En este caso Tipo E, para calcular la raíz cuadrada de 1000 se comienza escribiendo 1000 en la ventanilla. Luego se presiona en “Inv” y finalmente se presiona sobre x^2. El resultado es el siguiente:

31,622776601683793319988935444327

Esa raíz cuadrada de 1000 es sumamente útil en el cálculo de diferencias energéticas de la Escala Richter. Se debe a que la diferencia energética entre un grado Richter y el siguiente, es de justamente 31,62 veces. Y la diferencia energética entre 2 grados Richcter es de 1000 veces (es decir de 31,62 elevado al cuadrado).

Al pasar de un grado Richter al siguiente, se vá multiplicando la energía convertida por 31,62 veces. La serie puede ser de 31,62 luego 1000, enseguida 31623, luego 1000000, etc.

Salvo error u omisión.

Cordiales saludos
Rafael Meza